CFD Gittersorten

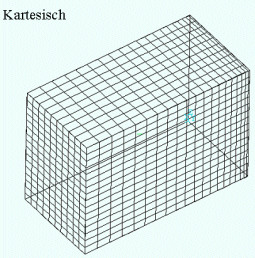
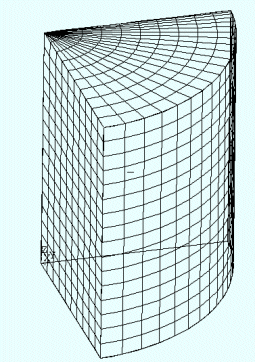
Kartesische Gitter

Das für numerische Methoden idealste Gitter ist das kartesische Gitter. Es besteht aus "Quads" bei zweidimensionalen und "Hexaehder" bei dreidimensionalen Gittern.

Die Zellen werden entlang der Raumachsen, X, Y und Z) aneinander gereiht.

Die Koordinaten jeder Zelle kann ausgehend von einem Ursprungspunkt mit Hilfe der Zelldimensionen (Länge, Breite und Höhe) und der Anzahl der Zellen entlang einer Achse ermittelt werden.

Ein verwandtes Gitter ist das sogenannte Zylinder-Polar-Gitter. Dabei wird in der Regel die Zylinderachse entlang Z geordnet. Y stellt die radiale und X die tangentiale Richtung dar.

Zur Abbildung komplexer Geometrien eignen sich diese Gitter nur bedingt. Eine häufig angewandte Annäherung stellt die Approximation der Geometrie in Form von Treppen. Bei einem ausreichend feinen Gitter - entsprechend sind die Treppen nicht zu grob - lassen sich Druckverluste und globale Strömungsbilder gut ermitteln. Dies gilt jedoch nicht bei Wärmetransport, da die Korrekte Abbildung der Grenzschicht für eine genaue Berechnung maßgeblich ist.

Körperangepasstes Gitter

Kartesische Zellen werden zur Abbildung von Krümmungen verformt. Die Struktur des Gitters bleibt jedoch vergleichbar mit einem kartesischen Gitter. Dies bedeutet, dass die Gitterlinien durchgehen sind. Sin sind jedoch nicht parallel zur den Raumachsen X,Y und Z. Stattdessen verformen sie sich entlang der lokalen Koordinaten i, j und k.

Die räumliche Position der Zelleckpunkte (Knoten) wird mit den X,Y und Z-Koordinaten angegeben.

Diese Gitter verursachen einen höheren Rechenaufwand je Iteration ermöglichen aber eine gute Abbildung komplexere Geometrien.

Durch die angesprochen numerische Einschränkungen sind Grenzen der Verformung/Verzerrung der Zellen gesetzt, die die Gittergenerierung erschweren. Wird in einem Gitter eine Zelle zu stark verzerrt kann es dazu führen, dass die Berechnung nicht erfolgen kann (Divergenz).

Multiblock Gitter

Werden mehrere körperagepasste Gitterteile, jeweils mit einem eigenen i, j und k Koordinatensystem, aneinander gereiht entsteht ein Multiblock-System. Ein solches System bietet wesentlich mehr Flexibilität bei der Abbildung komplexer Geometrien an.

Die Grenzen der Zellendeformation bleiben jedoch bestehen.

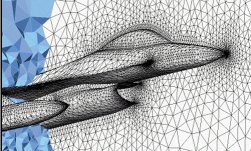
Unstrukturiertes Gitter

Als Lösung zur schnellen Abbildung komplexer Geometrien werden unstrukturierte Gitter eingesetzt. Sie bestehen aus Tetraehder, Pyramiden und Polyehder.

Auch diese Zellen unterliegen der Deformationsgrenzen. Sie lassen sich jedoch relativ schnell einhalten wenn die Zellkantenlängen ausreichend kleine sind, d.h. eine hohe Auflösung angewandt wird.

Wird diese notwendig hohe Auflösung nicht überall im Lösungsgebiet benötigt kann eine allmähliche Gittervergröberung vorgenommen werden.

Der Nachteil dieser Gitter ist, dass sehr große Gitter entstehen, die zu einem erhöhtem numerischen Aufwand und langen Rechenzeiten führen.

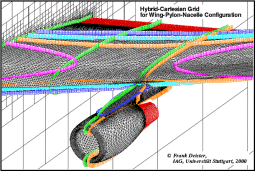
Hybride Gitter

Um die Vorteile strukturierter Gitter mit denen von unstrukturierten Gittern zu kombinieren werden "hybride" Gitter eingesetzt.

Im wandnahen Bereich, zum Beispiel, wo besonders feine Zellen benötigt werden, werden Hexaehder angewandt. Während andere Regionen mit Hilfe von Prismen und Pyramiden aufgelöst werden.